Unfortunately there is no simple "one liner" that will shuffle an array in javascript. All to often I see people advising to use:

sort(function() { Math.random() - 0.5 }))

However, this does not shuffle the array. First, let's take a look at what does work. It's called the Fisher-Yates shuffle and looks like this in javascript:

function shuffleSort(a) {
  for(var i = 0; i < a.length; i++) {
    var r = Math.floor(Math.random() * (i + 1));
    var t = a[i];
    a[i] = a[r];
    a[r] = t;
  }
}

Why doesn't sorting with a random comparator work? It all depends on the algorithm and what I found really interesting is how each sort algorithm has a different "order bias" which can be made into an image by mapping original position on the x and final position on the y and shading the probability from 0.0 cyan and max percent magenta. Also, in the images below I've expanded the image size so each original-final is 2x2 pixels and they are seperated by white space. Each test was run on an array initialized to [0..99] sorted and run for 1 million iterations. If you want to play around with the code it's all here and an example page with images here.

Fisher-Yates shuffle

function shuffle(a) {
  for(var i = 0; i < a.length; i++) {
    var r = Math.floor(Math.random() * (i + 1));
    var t = a[i];
    a[i] = a[r];
    a[r] = t;
  }
}

As expected this produces a pretty flat image with a probability range [0.009627, 0.010367] after 1 million iterations.

Random Sort

function randomSort(a) {
  a.sort(function() { return Math.random() - 0.5 });
}

Probability range [0.000965, 0.033447] after 1 million iterations.

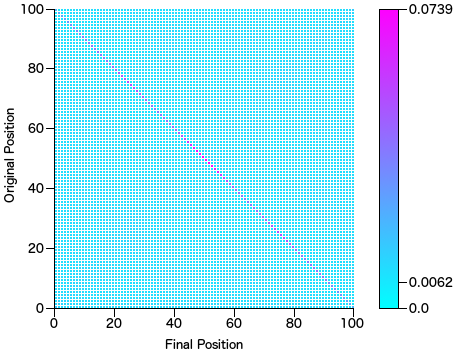
Quick Sort

Probability range [0.006287, 0.073966] after 1 million iterations. Just from the looks of it quick sort seems to have the worst performance in the center of the array getting the least shuffle.

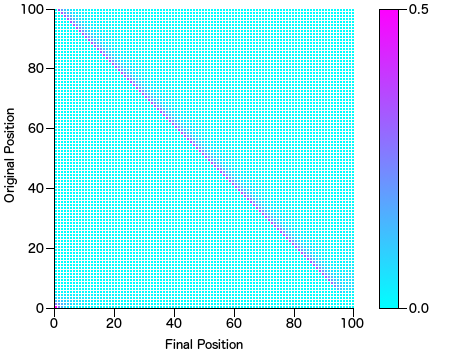
Bubble Sort

function bubbleSort(a) {
  var l = a.length;
  var i, j, s, t;
  for (i = 0; i < l; i++) {
    for (j = 0, s = l-i-1; j < s; j++) {
      if (Math.random() < 0.5) {
        t = a[j];
        a[j] = a[j+1];
        a[j+1] = t;
      }
    }
  }
}

Probability range [0 0.500113] after 1 million iterations, which is amazing that after that many trials there were still positions that certain numbers never made it to.

At first I thought my sort was off, but then I realized to move 0 from first position to last position requires the comparator (in this case Math.random() - 0.5 < 0.0) to be less than 0.5 99 times in a row. Also, for 9 to remain in last position is 0.5 percent chance that when i=0 and j=9 that Math.random() < 0.5 is false. I double checked this for arrays size 10 in length and the probability range was as expected [0.001923 0.500352] since Math.pow(0.5, 9) == 0.001953125.

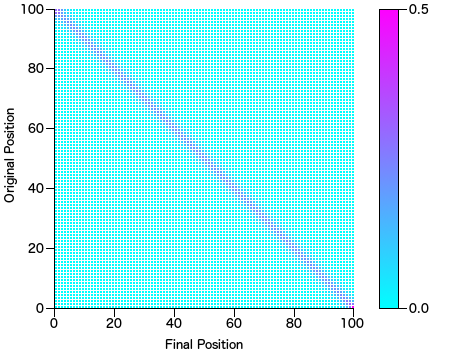
Selection Sort

function selectionSort(a) {
  var i, j, m, t;
  var l = a.length;
  for (i = 0; i < l; i++) {
    m = i;
    for (j = i+1; j < l; j++) {
      if (Math.random() < 0.5) m = j;
    }
    if (i != m) {
      t = a[i];
      a[i] = a[m];
      a[m] = t;
    }
  }
}

Probability range [0 0.500113] after 1 million iterations. Selection sort has some similar problems that bubble sort does. Consider an array a=[0..9] what is the probability that 9 which started in the last position will end up in the first position? If the array was shuffled it should be 0.1, right? But instead for selection sort it is 0.5. Because the only way for 9 to move to the front is when i=0 and j=9 the comparator (in this case Math.random() - 0.5 < 0.0) is less than zero which happens half the time.

Insertion Sort

function insertionSort(a) {
  var l = a.length;
  var i, j, t;
  for (i = 0; i < l; i++) {
    t = a[i];
    for (j = i-1; j > -1 && Math.random() < 0.5; j--) {
      a[j+1] = a[j];
    }
    a[j+1] = t;
  }
}

Probability range [0 0.499359] after 1 million iterations.